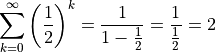16.3 Geometric Series¶
Consider the series:
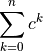
for some 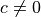 and
and 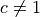 .
.
We can calculate the sum by simply multiplying the series by 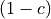 :
:
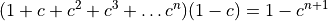
Dividing both sides by 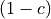 yields:
yields:
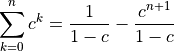
What happens as we increase 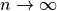 ?
?
If
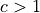 , then the term on the right will blow up and also increase
off to infinity. This isn’t very interesting, so let’s ignore it for now.
, then the term on the right will blow up and also increase
off to infinity. This isn’t very interesting, so let’s ignore it for now.If
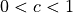 , then the term on the right will get smaller and
smaller and eventually become 0.
, then the term on the right will get smaller and
smaller and eventually become 0.
This second case is most interesting, because it gives us:
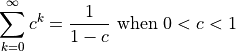
Note that the 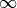 symbol is not a number. In this context, it is
the idea that
symbol is not a number. In this context, it is
the idea that  keeps increasing on and on forever.
keeps increasing on and on forever.
As an example, suppose 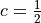 :
: