2.1 Curve Sketching¶
Definitions¶
- critical point
A point where the first derivative is zero.
- local minimum
A point where the first derivative is zero, and the second derivative is positive on both sides.
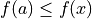 for all points within a certain region if the minimum is at
for all points within a certain region if the minimum is at
 .
.- local maximum
A point where the first derivative is zero, and the second derivative is negative on both sides.
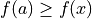 for all points within a certain region if the maximum is at
for all points within a certain region if the maximum is at
 .
.- absolute maximum/minimum
The minimum or maximum for all the points in the range.
- extreme point
A local minimum or a maximum.
- point of inflection
A point where the second derivative changes sign. This can occur where the second derivative is undefined or zero.
- even function
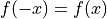
- odd function
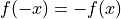
Curve Sketching Process¶
- Step 1
Identify where
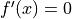 (Critical points.) The tangent line is
zero here.
(Critical points.) The tangent line is
zero here.- Step 2
Where
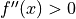 , it is concave upward. Where
, it is concave upward. Where 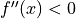 , it
concave downward.
, it
concave downward.- Step 3
Where
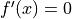 , If
, If 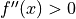 , then it is a local
minimum point. If
, then it is a local
minimum point. If 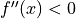 , then it is a local maximum point.
, then it is a local maximum point.- Step 4
If
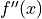 changes sign (at zero or undefined points) it is a
point of inflection.
changes sign (at zero or undefined points) it is a
point of inflection.- Step 5
Even and odd functions need only be investigated for positive x. Flip or rotate it when done.

