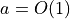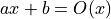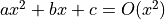Big O Notation¶
Before we get into lists, I want to emphasize a concept you are going to hear me talk about again and again.
When we consider algorithms, that is, miniature programs, we want to figure out if it is going to take a long time to run, or if it is going to us a lot of memory. We ask ourselves what will happen if we have 2x, or 10x, or 1,000x as much data, and we apply these simple algorithms.
Big O Notation is the system we have come up with to represent the complexity of the algorithm, and it is used to figure out what the complexity of new algorithsm are.
Why We Want Big O Notation¶
When we are considering algorithms, we want a simple tool that will tell us how quickly the algorithm will blow up, either in terms of computation time or memory usage. One algorithm might work fine for 10 or 20 elements, but when we try to apply it to millions, it will take more time than the universe has been around. Another algorithm will be slow for 10 or 20 items, but not much slower for thousands or even millions of items.
There are two scales we worry about as programmers: The few and the many. By few, I mean numbers that are not hard for a computer to deal with – numbers typically below 100. By many, I mean numbers that may be hard for humans to comprehend – millions or billions or more.
Big O will tell us what will happen if we try to take the algorithm to extremes. It will give us a clue whether this algorithm is just good for small numbers of items or astronomical numbers.
When we use Big O notation, we tend to see the following behaviors:
Constant:
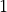 These algorithms will take roughly the same time whether
you have a few items or many. This may seem like a fantasy, but we’re going
to see it again and again for the most common algorithms.
These algorithms will take roughly the same time whether
you have a few items or many. This may seem like a fantasy, but we’re going
to see it again and again for the most common algorithms.Logarithmic:
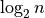 . You might wonder how these arise. It has to
do with algorithms that divide the data into half and only look at one half,
and then divide that in half and so on until it finds what it is looking
for.
. You might wonder how these arise. It has to
do with algorithms that divide the data into half and only look at one half,
and then divide that in half and so on until it finds what it is looking
for.Root:
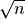 (Includes other fractional powers.)
(Includes other fractional powers.)Linear:
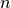 These algorithms increase according to the number of
items. Anything with this complexity or larger is undesirable for very large
numbers. For instance, if it takes 1 hour to process a million items, it
will take over a month for a billion and over a hundred years for a
trillion. Or, in terms of memory, if you can process a thousand records with
$100 of memory, you’ll need $100,000 to process a million records, and
$100,000,000 to process a billion.
These algorithms increase according to the number of
items. Anything with this complexity or larger is undesirable for very large
numbers. For instance, if it takes 1 hour to process a million items, it
will take over a month for a billion and over a hundred years for a
trillion. Or, in terms of memory, if you can process a thousand records with
$100 of memory, you’ll need $100,000 to process a million records, and
$100,000,000 to process a billion.n-log-n:
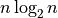 Arises surprisingly often, usually for sorting a
list of items in-place. Although it isn’t much worse than linear, it is
worse than linear.
Arises surprisingly often, usually for sorting a
list of items in-place. Although it isn’t much worse than linear, it is
worse than linear.Quadratic:
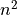 and other powers. (We might call the other powers
‘polynomial’.) These algorithms are quite sensitive to large numbers.
Doubling the number of items will quadruple the run time or memory usage.
and other powers. (We might call the other powers
‘polynomial’.) These algorithms are quite sensitive to large numbers.
Doubling the number of items will quadruple the run time or memory usage.Exponential:
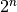 These are bizarrely bad algorithms. If you end up
writing an exponential algorithm and you didn’t put limits on the number
of records you process, you might end up costing people their jobs. To give
you an idea of why this is bad, let’s say it takes 1 hours to process 100
records. With exponential behavior, if you simply double the number of
records, it will take 4 hours. But it you increase the number of records to
10x, it will take a month. If you tried increasing it by 100 times, you’re
looking at taking 10,000,000,000,000,000 (10 quadrillion = 10^16) ages of
the universe. In terms of memory, if it takes $100 of memory to process 100
records, you’re looking at $400 to process twice as much, $102,400 for ten
times, and an incomprehensible amount of money for 100 times.
These are bizarrely bad algorithms. If you end up
writing an exponential algorithm and you didn’t put limits on the number
of records you process, you might end up costing people their jobs. To give
you an idea of why this is bad, let’s say it takes 1 hours to process 100
records. With exponential behavior, if you simply double the number of
records, it will take 4 hours. But it you increase the number of records to
10x, it will take a month. If you tried increasing it by 100 times, you’re
looking at taking 10,000,000,000,000,000 (10 quadrillion = 10^16) ages of
the universe. In terms of memory, if it takes $100 of memory to process 100
records, you’re looking at $400 to process twice as much, $102,400 for ten
times, and an incomprehensible amount of money for 100 times.
Here’s a brief run-down on how these algorithms behave. Let’s suppose that it takes 1 second to process 10 records.

(1 year is about 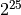 seconds.)
seconds.)
Or, put another way, let’s say it takes $1 of memory to process 10 records. Here’s how much memory you would have to but to process a different number of records for different Big-O’s.
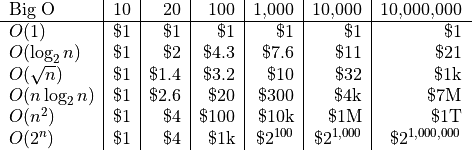
I want to point out to you something you probably didn’t notice. The
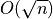 is actually better than
is actually better than 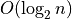 when we only
double
when we only
double n. Sometimes people choose bad algorithms for small n because
it gives better results. You’ll see in practice many fancy algorithms have
available several different algorithms to use, and will switch algorithms
based on the size of the data set. For smaller n, it will use less
efficient algorithms that wouldn’t work well for larger n.
Formal Definition of Big O Notation¶
Mathematically, we say that 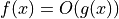 as
as 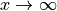 when f(x) < Mg(x) for all
when f(x) < Mg(x) for all 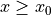 . In other words, there
is some number
. In other words, there
is some number 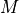 that you can multiply
that you can multiply 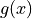 by that is always
larger than the corresponding
by that is always
larger than the corresponding 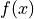 beyond some value of
beyond some value of 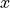 .
.
What this gives us is a function (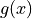 ) that describes how
) that describes how
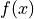 behaves as
behaves as 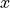 gets larger and larger, dropping any
coefficient that really doesn’t help us understand the behavior.
gets larger and larger, dropping any
coefficient that really doesn’t help us understand the behavior.
It’s rather trivial to convert 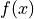 into
into 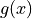 : Just keep the
term that blows up the biggest and drop the coefficients.
: Just keep the
term that blows up the biggest and drop the coefficients.
Examples:
Properties of Big O Notation¶
Let’s now look at some properties of Big O.
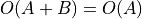 when
when 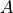 blows up faster. (
blows up faster. (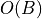 otherwise.) Thus, we should never see Big O of sums.
otherwise.) Thus, we should never see Big O of sums.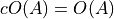 when
when  is some constant number.
is some constant number.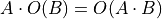
We Use Two Big O’s¶
There are two things we care about when we are looking at algorithms and judging how bad they get.
How long the algorithm takes to run.
How much memory it requires to run.
Since we can often trade memory for time, and time for memory, we should really consider both of these parameters. We’ll develop a separate Big O for each one.
How to Calculate Complexity of an Algorithm¶
Calculating Big O isn’t hard, but you have to be careful not to make a mistake, just like when you are solving math problems.
These are the general steps I use to calculate Big-O for time:
First, ignore all linear code. That is, if you have a chunk of code with no loops and no function calls, consider it a single line of code.
When calling a function, the Big O for that call is the same as the Big O for the function.
Next, when considering loops, count the number of times it will loop and consider each branch separately. If a loop has branches inside, one that calls a function and one that doesn’t, you’ll have to count the number of times it will call the function and the number of times it doesn’t.
To calculate it for memory, I look for the maximum amount of memory used to run the algorithm.
Each variable or slot of memory takes up 1 unit, no matter its actual size.
Each function call also takes up 1 slot of memory.
For recursive functions, we look at how deep it might go. (If we have tail recursion, it would be constant. But we don’t in Python, so we have to know how deep it will go.)
We should also consider how big the input and output is. IE, if you’re looking up a record in an array, then you have to store the records in memory in one shape or another.
Example 1: Recursive Fibonacci¶
Let’s do a few examples, using some recursive functions and some loops.
Calculating Big O for the Fibonacci involves us analyzing the code. Here is a simple version:
def fibonacci(n):
if n <= 0: return 0
elif n == 1: return 1
else: return fibonacci(n-1) + fibonacci(n-2)
We’re going to calculate this by calculating the number of function calls
based on the parameter n. We’ll call this function 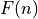 .
.
If n<=1, then 1 call is made. 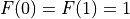 .
.
If n==2, then we have 3 calls: 1 for 2, 1 for 1, and another for
0. 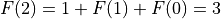
If n==3, then we have 5 calls: 1 for 3, 3 for 2, and 1 for 1.
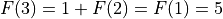 .
.
For any n>1, we have the formula F(n) = 1 + F(n-1) + F(n-2), which
itself is a kind of Fibonacci sequence.
We’ll use Proof by Induction to calculate F. If you haven’t seen my Basic
Mathematics video on Proof by Induction, you can watch it later.
Here’s how proof by induction works. First, we make up an answer. Then, we
prove that the answer works for 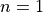 . Then we prove that the answer
works for
. Then we prove that the answer
works for 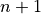 , assuming it works for
, assuming it works for 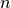 .
.
Let’s assume that recursive fibonacci is exponential: 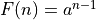 .
.
We’re skipping n=0. It’s just 1 anyway, which will be lost in Big O
notation.
This works for 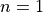 as
as 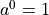 .
.
What about for 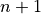 ?
?
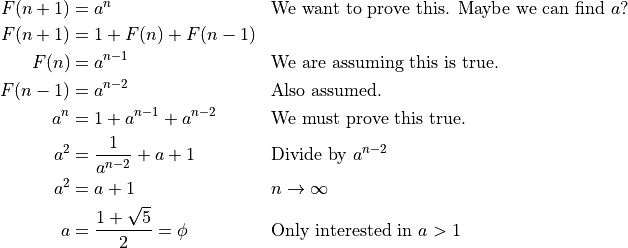
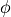 is the Golden Ratio, about 1.618.
is the Golden Ratio, about 1.618.
So, as 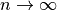 ,
, 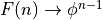 .
.
We’ll use 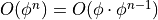 to drop the useless
to drop the useless 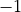 . That’s how much
time it will take to calculate the Fibonacci element for large n. This is
quite bad, and I don’t recommend doing it for anything other than a learning
exercise.
. That’s how much
time it will take to calculate the Fibonacci element for large n. This is
quite bad, and I don’t recommend doing it for anything other than a learning
exercise.
How much memory does recursive fibonacci use? The answer is rather easy. At
most, it will have n frames on the stack. So it is 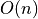 .
.
Example: Fibonacci Loop¶
Let’s examine the Fibonacci loop.
def fibonacci(n):
if n <= 0: return 0
if n == 1: return 1
prev_prev = 0
prev = 1
while n > 1:
result = prev + prev_prev
prev_prev = prev
prev = result
n = n - 1
return result
How many times do we need to iterate through the loop? The answer is simple:
n times! Since there are no function calls or branches inside the loop,
there is nothing more to consider. This function is 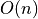 . This is
significantly better than the previous recursive implementation, but it is
still not very good for calculating very large
. This is
significantly better than the previous recursive implementation, but it is
still not very good for calculating very large n.
The memory usage of this algorithm, however, is excellent. It doesn’t matter
how large n is, it will always use the same three variables, and never
make any function calls. So it is 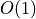 in terms of memory.
in terms of memory.
Example: Cached Fibonacci¶
Can we do better? We could possibly store the first million terms of the
Fibonacci sequence in memory, trading speed for memory. Each term would be an
integer, possibly quite large, but as long as n isn’t too big, it would be
O(n) to store the first n terms in memory. But it will be very fast!
O(1) in fact to retrieve any of thise first n terms!
Perhaps you can store only two adjacent terms spread out. So you store
fibonacci(100) and fibonacci(101), and then if you want to calculate
fibonacci(102) you just look up the previous two terms. This would reduce
the amount of memory required by how far you space them apart. But this would
only reduce them by a fraction, so it is still 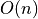 in memory.
Calculating would still only take
in memory.
Calculating would still only take 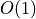 time, since at most you’d have
to calculate 98 terms for any
time, since at most you’d have
to calculate 98 terms for any n.
This is an example where what seems like a brilliant optimization doesn’t really solve the problem at hand. If you’re going to store some fraction of the fibonacci series in memory, then you’re getting O(1) time and O(n) memory usage.
Perhaps you want to spread out the terms that are stored in memory as n increases. You could get square root or logarithmic memory in such a case, but that would increase the amount of time from constant to logarithmic or square root or something like that.
Depending on what you intend to do with it, how much time you have, and how much memory you are willing to buy, you’ll have to find the right trade off.
More Possibilities¶
Or we can find better algorithms. (Look up Linear Recurrence if you’re interested.)
Or we can calculate estimates using even more math.
Conclusion¶
People poo-poo Big-O notation as some sort of interview exercise that’s used to keep people out of the industry. The truth is, I used Big-O all the time on my job. I had to know what the behavior of different algorithms were, debate with my colleagues about the merits of one algorithm versus another, and find new algorithms. We would often have discussions in the halls where we compared Big-O for various algorithms, and when you’re sifting through hundreds of possibilities and variations, being able to quickly find the Big-O of an algorithm, both for time and memory, was incredibly important.
If you want to work on my team, I’m going to ask you to learn Big-O and use it all the time. I’m going to ask you to describe the Big-O for the code you intend to write, and I’m going to expect you to check that I’m not making a miscalculation.
So don’t just study this to pass the interview. Study it to become a great software developer.
In the upcoming videos, I’m going to refer back to Big-O a lot as an explanation for why we do things the way we do.